
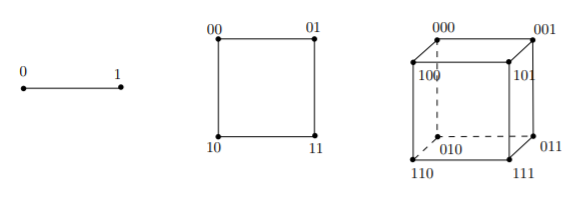
The extremal number defines the maximum number of edges in such a saturated graph,but we can also ask the converse question: what is the minimum number of edges in asaturated graph? To this end, the saturation number sat( H, G ) is defined as the minimumnumber of edges in a G -saturated subgraph of H. In particular, considerthe following definition, where E ( G ) represents the set of edges in a graph G : Definition 1.1.Ī subgraph H ′ of H is ( H, G ) -saturated if it is G -free, but the addition ofany edge in E ( H ) \ E ( H ′ ) to H ′ creates a copy of G. The extremal number also has a natural opposite formulation. In particular, the extremal number ex( H, G ) is defined as the maximum number of edges in a subgraph of ahost graph H that does not contains some forbidden graph G. Some further results on C 4-avoiding sets of edges which are connecting vertices of three consecutive levels of the hypercube can be found in 11. Thisresult sparked the study of what is now known as the extremal number. For small values of n, the exact number of edges in a largest C 4-free subgraph of Q n was determined in 7, 10. In 1941, Paul Tur´an proved one of the first important results in extremal graph theory,explicitly determining the maximum number of edges in a K r +1 -free subgraph of K n. We also improve the upper bound on the number of edges for 6-cycle-free subgraphs of the n-dimensional hypercube from the square root of 2 - 1 to 0.3755 times. From there,we suggest two general methods for constructing T -saturated subgraphs of Q n andprove nontrivial upper bounds for specific types of trees, including paths, generalizedstars, and certain caterpillars under a restriction on minimum degree with respect todiameter. We first present a general lower boundon the saturation number based on the minimum degree of non-leaves. We investigate bounds on the saturation numberof trees T in the n -dimensional hypercube Q n. The saturation number sat( H, G ) is the minimum number ofedges in an ( Kavish Gandhi and Chiheon KimJuly 16, 2018Ī graph H ′ is ( H, G )-saturated if it is G -free and the addition of any edge of H notin H ′ creates a copy of G. This is equivalent to draw a vertical line between s k and s k + 1, and then count the number of intersections with the edges of Q n. M 5 since there are 5 edges ( u, v) where u s 3 ( 010) and v s 4 ( 011). N ov Saturation Number of Trees in the Hypercube By symmetric, we only need to consider 1 k 2 n 1 (the left half). The congestion of an edge F equals the number of edges in G whose images. I do not know anything about the isoperimetric problem for these graphs, but there has likely been work done on the $n \leq 4$ cases, since those graphs also show up as other constructions.Aa r X i v. maps of independent copies of the guest graph within the hypercube. a graph with equal number of vertices and edges whose vertices can be. See, and various dimension specific pages there. The hypercube Qn is the graph whose vertices are the ordered n-tuples of zeros. By $n=5$, the polytopes begin to take shape as their own specific family and no longer have multiple names. $n=4$ is the 16-cell, also called a hexadecachoron in older books, and happens to be a cross-polytope (this does not continue in higher dimensions). Specific dimensional cases have different names. there is another equivalent recursive denition of the hypercube: the n-dimensional hypercube consists of two copies of the n 1-dimensional hypercube (the 0-subcube and the 1-subcube), and with edges between corresponding vertices in the two subcubes. See Conway, Burgiel and Goodman-Strass's "Symmetries of Things." Chapter 26 covers this, where they call them hemicubes, and draw some lovely pictures.
Since then, halfcube seems to have lost favour, and hemi-cube has become the name for a construction of quotienting out vertices, while the term demicube (or demihypercube if you want to be explicit about using hypercubes and not cubes) is reserved for the construction of deleting vertices of a hypercube. Conway & Sloane's "Sphere Packings, Lattices and Groups" references Coxeter's "Regular Polytopes" for the phrase "halfcube", but Coxeter only uses the notation $h\Pi_n$, saying $h$ can be taken to stand for half- or hemi-, for an arbitrary polytope $\Pi_n$ ) This construction is section 8.6 in Coxeter.


 0 kommentar(er)
0 kommentar(er)
